Cosmic-Rays
Introduction
Cosmic rays are charged particles that are born in the some most violent environments in our Universe. The cosmic rays that arrive at Earth are primarly composed of protons and alpha particles, with elements up to iron nuclei (and some heavier elements in trace amounts) in the mix. By studying the energy spectrum, arrival distribution, and composition of these particles, we can learn more about the origins of cosmic rays and the environments in which they travel to reach us. Ultimately, it is by understanding these smallest consituents of matter that we can get a better picture of the largest structures in our Universe.
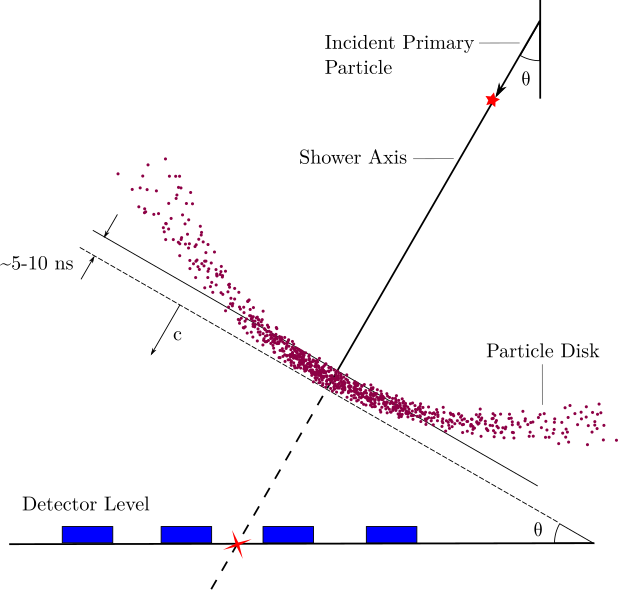
Primary cosmic ray particles with energies above 100 GeV incident at the top of the Earth’s atmosphere produce extensive air showers, characterized by a wide but thin disk of secondary particles (left) that travels at nearly the speed of light. The nature of the primary particle determines how the shower will evolve, allowing us to estimate its identity and energy with detectors on the ground. This is done using the relative timing and measured signals of the detector elements (blue boxes) as the air shower passes over the detector.
Image credit: Z. Hampel-Arias
Research with HAWC

My PhD research focused on making cosmic rays measurements with the HAWC Observatory, an air-shower experiment located near Puebla, Mexico on the slopes of Pico de Orizaba (right). HAWC comprises a total of 300 large water tanks, each being 7 meter high and 4 meter wide, and having four sensitive light collectors from which we make our measurements on cosmic-ray showers.
Photo credit: Z. Hampel-Arias
Energy Spectrum
In the energy range at which HAWC is sensitive to cosmic rays, the best measurements by other experiments are subject to either diminishing statistics or large systematic uncertainties. By limiting our data to only the best events, we were able to measure the cosmic ray spectrum, showing structure that had not been previously verified. This was done by harnessing the statistical technique discussed below as well as a validation of our methods using cosmic-rays blocked by the Moon, i.e. the Moon shadow.
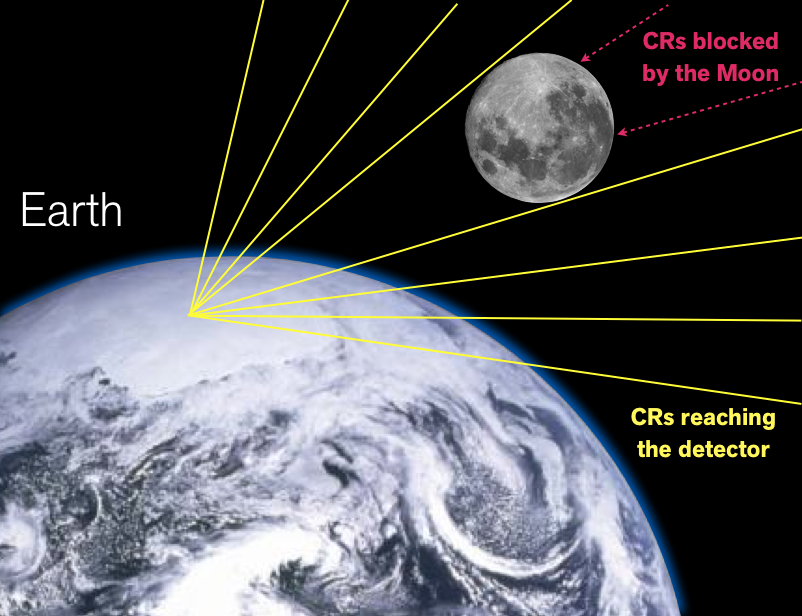
Since the Earth’s magnetic field bends cosmic-ray trajectories, the observed Moon shadow shifts with energy, allowing us to verify our energy and angular estimates. This cool animation shows this energy-depenent bending as low-energy protons interact with the geomagnetic field. In the video, some particles get stuck in the field, tracing out its shape as large arcs. Indeed, it’s these low energy particles that cause the aurorae! HAWC measures particles with much higher energy, but the same physics applies. The visualization was generated using my charged particle propagation tool found here.
Image credit: WIPAC
The results of this study were published as an Editor’s Suggestion in Phys. Rev. D. also available on the arXiv. We also harnessed the Moon shadow technique to measure the anti-proton to proton ratio, recently published in Phys. Rev. D, found here on the arXiv.
Anisotropy
Whereas the energy spectrum provides clues about the nature of particle accelerators, the arrival distribution of cosmic rays gives us an idea of where these particles are coming from. In addition to probing cosmic ray source distributions, as with the Moon shadow, we also get a glimpse into the intervening magnetic field structure of interstellar space. In collaboration with my HAWC colleagues, we recently published our study of the cosmic ray anisotropy at TeV energies in The Astrophysical Journal, found here on the arXiv.
Statistical Deconvolution
Introduction
In order to measure the cosmic ray energy spectrum, I used a deconvolution method called unfolding. Since not all showers reach the ground or trigger our detector, and the fact that our HAWC is, sadly, not perfect, we can take into account these measurement inefficiencies and biases to unfold an estimate of the true spectrum. Basically, we build what’s called a response function which connects the probability of a true cause that we want to estimate to produce a effect we can measure. This method is great for experimental situations where a perfect analytic form of this function is not known or easy to construct. Instead we build a matrix from simulation that allows us to do the unfolding. This method falls under the category of inverse problems, where for sets of causes \(c_{\mu}\) and effects \(e_j\), and a constructed response matrix \(\mathbf{R}\), we want to find \(\mathbf{M} \approx \mathbf{R}^{-1}\) such that
\[\mathbf{e} = \mathbf{R} \, \mathbf{c} \\ \mathbf{c} = \mathbf{M} \, \mathbf{e}\]D’Agostini in his 1995 paper developed a method that starts from Bayes’ Theorem to obtain an approximate form for \(\mathbf{R}^{-1}\). This iterative unfolding procedure is widely-used in the high-energy physics community (HEP) and has some advantages over other matrix inversion methods, for example in cases where no inverse actually exists.
PyUnfold

The code I designed for the HAWC cosmic ray measurement has been generalized for use beyond the HEP community
by myself and another astrophysicist (with some updates from D’Agostini’s original version),
and is now packaged as PyUnfold.
The project was recently published in the Journal of Open Source Software
also available on Zenodo.
Publications
For a list of my publications as a major contributor, see the relevant section in my Résumé page.
